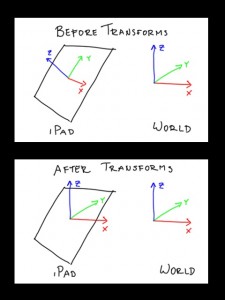Last time, I posted a starfield video which demonstrates an iPad being used to look around in a virtual 3D environment. So how is this done? The basic idea is to line up the xyz coordinate system of the iPad to the xyz coordinate system of the world. Well, the world doesn’t really have an xyz coordinate system, but we’ll call “z” the direction that lines up with gravity and “y” the direction that lines up with North.

The first step, as you might guess, is to use the iPad’s accelerometer and compass to find out what direction gravity and north are in. Then, it’s a matter of taking those to vectors and rotating everything so that the iPad’s z-direction (which is initially pointing perpendicular to the screen towards you) to line up with the gravity vector and the iPad’s y-direction (which is initially pointing to screen right) to line up with the north vector. Here are the steps involved:

• rotate z so that the iPad’s new xz-plane lines up with the gravity vector
• rotate y so that the iPad’s new z-direction lines up with gravity
• recalculate the north vector in this new coordinate system
• rotate z again so that the iPad’s new y-direction now points north

But how do you know how much to rotate by? Well, that’s where trigonometry comes in. Let’s call your gravity vector . If that happens to be <0, 0, -1>, that means your iPad is lying flat on a table or something and you wouldn’t have to do anything. But for anything else, you’ll want to line up your new xz-plane with this . In other words, you need to figure out the angle between and <1, 0>. You do this by taking the arctangent of Gy over Gx, or “atan2(Gy, Gx)”.

The rest is left as an exercise for the reader…

This entry was posted on Friday, April 23rd, 2010 at 6:00 am and is filed under Uncategorized. You can follow any responses to this entry through the RSS 2.0 feed. Both comments and pings are currently closed.